Основные теоремы двойственности
Двойственность в линейном программировании - принцип, заключающийся в том, что для каждой задачи линейного программирования можно сформулировать двойственную задачу.
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу линейного программирования, называемую двойственной или сопряженной по отношению к исходной или прямой. Связь исходной и двойственной задач заключается главным образом в том, что решение одной из них может быть получено непосредственно из решения другой.
Теория математического линейного программирования позволяет не только получать оптимальные планы с помощью эффективных вычислительных процедур, но и делать ряд экономически содержательных выводов, основанных на свойствах задачи, которая является двойственной по отношению к исходной ЗЛП.
Произвольную задачу линейного программирования можно определенным образом сопоставить с другой задачей линейного программирования, называемой двойственной. Первоначальная задача является исходной. Эти две задачи тесно связаны между собой и образуют единую двойственную пару.
Различают симметричные, несимметричные и смешанные двойственные задачи.
Виды двойственных задач и составление их математических моделей
- 1. Симметричные двойственные задачи
Дана исходная задача
L (x) = c1x1 + c2x2 +…+ cnxn → max
при ограничениях:
a11x1 + a12x2 + … + a1nxn ≤ b1 │ y1 ,
a21x1 + a22x2 + … + a2nxn ≤ b2 │ y2 ,
………………………………………
am1x1 + am2x2 + … + amnxn ≤ bm │ ym ,
xj ≥0 , j = 1,n , i = 1,m.
Задача дана в неканоническом виде. Составим математическую модель двойственной задачи, для этого:
- каждому неравенству системы ограничений исходной задачи приводим в соответствие переменную yi ;
- составляем целевую функцию, коэффициентами которой являются свободные члены системы ограничений исходной задачи;
- составляем систему ограничений. Коэффициенты системы ограничений образуют транспонированную матрицу коэффициентов системы ограничений исходной задачи. Знаки неравенств меняются на противоположные;
- свободными членами системы ограничений являются коэффициенты целевой функции исходной задачи. Все переменные двойственной задачи неотрицательны.
Математическая модель двойственной задачи имеет вид
S(y) = b1y1 + b2y2 +…+ bmym → min
при ограничениях:
a11y1 + a12y2 + … + am1ym ≤ c1 ,
a12y1 + a21y2 + … + am2ym ≤ c2 ,
………………………………………
a1ny1 + a2ny2 + … + amnym ≤ cn ,
yj ≥0 , i = 1,m , j = 1,n.
- 2. Несимметричные двойственные задачи
Дана исходная задача
L (x) = c1x1 + c2x2 +…+ cnxn → max
при ограничениях:
a11x1 + a12x2 + … + a1nxn = b1 │ y1 ,
a21x1 + a22x2 + … + a2nxn = b2 │ y2 ,
………………………………………
am1x1 + am2x2 + … + amnxn = bm │ ym ,
xj ≥0 , j = 1,n .
Задача дана в каноническом виде. Составим математическую модель двойственной задачи.
Для ее составления пользуемся тем же правилом, что и для составления симметричной задачи, с учетом следующих особенностей:
- ограничениями двойственной задачи будут неравенства. Если в целевой функции двойственной задачи требуется найти минимум, то знак неравенства ≥, если максимум, то ≤ ;
- переменные yi - произвольные по знаку.
Математическая модель двойственной задачи имеет вид
S(y) = b1y1 + b2y2 +…+ bmym → min
при ограничениях:
a11y1 + a21y2 + … + am1ym ≥ c1 ,
a12y1 + a22y2 + … + am2ym ≥ c2 ,
………………………………………
a1ny1 + a2ny2 + … + amnxn ≥ cn ,
yj ≥0 , i = 1,m , j = 1,n.
yi – произвольные по знаку, i = 1,m.
- 3. Смешанные двойственные задачи
Математическая модель исходной задачи имеет условия симметричных и несимметричных задач. При составлении двойственной задачи необходимо выполнять правила симметричных и несимметричных задач.
2. Основные теоремы двойственности
ТЕОРЕМА 1. Если одна из двойственных задач имеет оптимальное решение, то другая также имеет оптимальное решение, причем для любых оптимальных решений X и Y выполняется равенство
L(x)max = S(y)min.
Если одна из двойственных задач неразрешима ввиду того, что
L(x)max → ∞ (или S(y)min → - ∞), то другая задача не имеет допустимых решений.
Основная теорема двойственности даёт правило нахождения оптимального решения двойственной задачи по оптимальному решению исходной задачи. Для нахождения оптимального решения двойственной задачи необходимо найти оптимальное решение исходной задачи симплекс-методом. Оптимальное значение двойственной переменной равно соответствующей оценке последней симплекс-таблицы плюс коэффициент целевой функции исходной задачи.
ТЕОРЕМА 2. Для оптимальности допустимых решений X и Y пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений
Xопт j *( ∑(aij*yопт i) - cj ) = 0,
yопт i ( ∑(aij*xопт j) - bi ) = 0.
Теоремы позволяют определить оптимальное решение одной из пары задач по решению другой.
ТРЕТЬЯ основная теорема двойственности (теорема об оценках).
Значения переменных в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов системы ограничений – неравенств прямой задачи на величину :
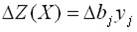
Диапазон изменения компонент вектора , в котором сохраняется оптимальный базис, называется областью устойчивости оптимальных оценок.
Экономический смысл первой теоремы двойственности следующий. План производства и набор ресурсов оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции , равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов . Для всех других планов прибыль от продукции всегда меньше или равна стоимости затраченных ресурсов , т.е. ценность выпущенной продукции не превосходит суммарной оценки затраченных ресурсов. Значит, величина характеризует производственные потери в зависимости от рассмотренной производственной программы и выбранных оценок ресурсов.
Для задачи оптимального использования сырья это уравнение показывает, что при изменении i-го ресурса оптимальный доход является линейной функцией от его приращения, причем коэффициентом служит уi — i-я компонента оптимального решения двойственной задачи.
Если yi мало, то значительному увеличению i-го ресурса будет соответствовать небольшое увеличение оптимального дохода и ценность ресурса невелика.
Если yi = 0, то при увеличении i-го ресурса оптимальный доход остается неизменным и ценность этого ресурса равна нулю. В самом деле, сырье, запасы которого превышают потребности в нем, не представляет ценности для производства и его оценку можно принять за нуль.
Если уi велико, то незначительному увеличению i-го ресурса будет соответствовать существенное увеличение оптимального дохода и ценность ресурса высока. Уменьшение ресурса ведет к существенному сокращению выпуска продукции.
Переменную уi считают некоторой характеристикой ценности i-го ресурса. В частности, при увеличении i-го ресурса на единицу (Δbi = 1) оптимальный доход возрастает на yi, что позволяет рассматривать yi как "условную цену", оценку единицы i-го ресурса, объективно обусловленную оценку.
Так как уi представляет частную производную от оптимального дохода по i-му ресурсу, то уi характеризует скорость изменения оптимального дохода при изменении i-го ресурса.